5351. Кактус
Кактус – это связный
неориентированный граф, в котором каждое ребро лежит не более чем на одном
цикле. Интуитивно кактус - это обобщение дерева, в котором разрешены некоторые
циклы. Вам следует проверить, является ли заданный граф кактусом или нет.
Важное отличие кактуса от дерева состоит в том, что кактус может иметь
некоторое количество остовных подграфов, которые также являются кактусами.
Количество таких подграфов (включая сам граф) определяет кактусность графа (для
дерева это число равно единице). Кактусность графа, не являющегося кактусом,
равно нулю.
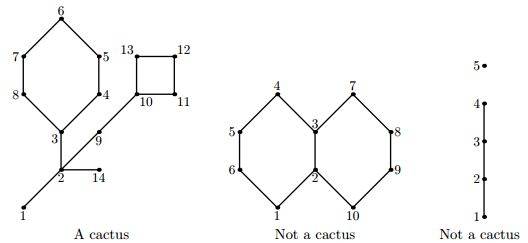
Кактусность
первого графа на рисунке равно 35. Второй граф не является кактусом, так как
ребро (2, 3) лежит на двух циклах. Третий граф не является кактусом, так как он
несвязный.
Вход. Первая строка содержит два целых
числа n и m (1 ≤ n ≤
20000, 0 ≤ m ≤ 1000).
Здесь n – количество вершин в графе.
Вершины пронумерованы от 1 до n.
Ребра графа представлены множеством реберно непересекающихся путей, где m – количество таких путей.
Каждая из следующих m строк содержит
путь в графе. Путь начинается с целого числа ki (2 ≤ ki
≤ 1000), за которым следует ki
целых чисел от 1 до n. Эти ki чисел задают вершины пути.
Путь может проходить по одной вершине несколько раз, но каждое ребро будет
задано лишь один раз во всех входных данных. Граф не содержит мультиребер
(между парой вершин находится не более одного ребра).
Выход. Выведите
одно число – кактусность графа. Отметим, что кактусность может быть большим
числом.
|
Пример
входа |
Пример
выхода |
|
14 3 9 1 2 3 4 5 6 7 8 3 7 2 9 10 11 12 13 10 2 2 14 |
35 |
РЕШЕНИЕ
графы –
поиск в глубину
Анализ алгоритма
Граф не является
кактусом, если:
·
существует ребро, принадлежащее более одному циклу;
·
граф не является связным
Для каждого
ребра графа в списке смежности добавим поле, в котором будем отмечать факт
принадлежности ребра некоторому циклу.
В массиве in
будем хранить адреса ребер, по которым идет поиск в глубину: если dfs движется
вперед, то заносим ребро в in, если назад – то выталкиваем ребро из in.
Очевидно, что
при удалении ребра – моста из графа он перестает быть связным, а следовательно
и кактусом. Цикл графа остается кактусом, если из него удалить только одно
ребро. Рассмотрим цикл, содержащий c
ребер. Он имеет c + 1 остовное
поддерево, являющихся кактусами (из цикла можно удалить одно из ребер, или не
удалять ребра вовсе).
Таким образом
для нахождения кактусности графа следует найти размеры всех его циклов q1, q2, …, qk
и вычислить произведение q = (q1 + 1) * (q2 + 1) * … * (qk + 1), которое является
большим числом.
Пример
Кактусность
графа
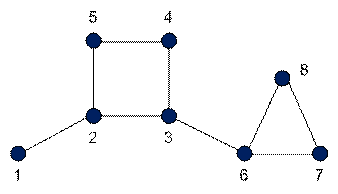
равна 5 *4 = 20,
так как он имеет два цикла размерами 4 и 3.
По окончанию
поиска в глубину на графе состояние списка смежности будет следующим:
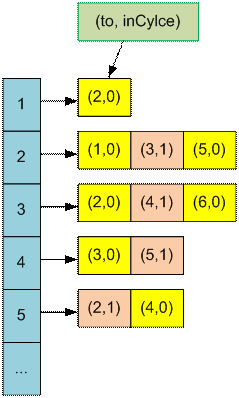
Обработан цикл 2
→ 3 → 4 → 5 → 2 (именно в таком направлении). В
обратном направлении, из вершины 2 в вершину 5 поиск не пойдет, так как на
момент обработки ребра 2 → 5 вершина 5 уже будет черной.
Реализация алгоритма
Объявим список смежности g для хранения графа. Для каждого
ребра (хранимого в структуре Edge) добавим информацию – принадлежит ли оно
некоторому циклу.
struct Edge
{
int to;
int inCycle;
Edge(int to, int inCycle) : to(to), inCycle(inCycle) {}
};
vector<vector<Edge>
> g;
vector<Edge
*> in;
vector<int> used;
Ответ задачи является длинным числом,
храним его в массиве result.
char result[10000];
Умножене длинного числа, хранящегося в массиве result, на q.
void mult(int
q)
{
int i, carry
= 0;
for(i = 0; i
< lres; i++)
{
int t = q *
result[i] + carry;
result[i] = t % 10;
carry = t / 10;
}
while (carry
> 0)
{
result[i++] = carry % 10;
carry /= 10;
lres++;
}
}
Вывод длинного числа result.
void print(void)
{
for(i = lres
- 1; i >=0; i--)
printf("%d",result[i]);
printf("\n");
}
Поиск в глубину из вершины v.
void dfs(int
v, int prev)
{
int i;
if (!f) return;
used[v] = 1;
for(i = 0; i
< g[v].size(); i++)
{
Рассматриваем ребро edge, исходящее из вершины v.
Edge &edge = g[v][i];
int to =
edge.to;
if (to ==
prev) continue;
Если ребро edge ведет в еще не посещенную вершину to, то запускаем поиск в глубину из to. Поддерживаем
массив in.
if
(used[to] == 0)
{
in.push_back(&edge);
dfs(to,v);
in.pop_back();
}
else
Вершина to серая. Встретился цикл. Ищем его размер q, увеличенный на 1. Все ребра, входящие в цикл, отмечаем как
принадлежащие циклу. Если при обработке текущего цикла некоторое его ребро уже
было ранее отмечено как входящее в цикл, то установится f = 0, и кактусность текущего графа
равна 0.
if
(used[to] == 1)
{
f &= !edge.inCycle;
edge.inCycle = 1;
int q =
2;
int ind
= in.size() - 1;
while(in[ind]->to
!= edge.to)
{
f &= !in[ind]->inCycle;
in[ind]->inCycle = 1;
q++;
ind--;
}
Умножаем ответ на задачу – длинное
число на q.
mult(q);
}
if (!f) return;
}
Красим черным цветом вершину v.
used[v] = 2;
};
Основная часть программы. Читаем
граф, заполняем список смежности g. Ребра графа неориентированные.
scanf("%d %d",&n,&m);
g.resize(n+1);
for(i = 0; i < m; i++)
{
scanf("%d",&len);
scanf("%d",&s);
for(j = 1; j
< len; j++)
{
scanf("%d",&e);
g[s].push_back(Edge(e,0));
g[e].push_back(Edge(s,0));
s = e;
}
}
Инициализация. Значение f будет оставаться равным 1, пока не
встретится двух циклов с общим ребром. То есть если установится f = 0, то граф не является кактусом.
used.resize(n+1);
f = 1;
Занесем в начало стека in фиктивное
ребро (ребро, ведущее в вершину 1).
Edge e(1,0);
in.push_back(&e);
Запускаем поиск в глубину из вершины
1.
dfs(1,-1);
Граф не будет кактусом, если не все его
вершины посещены. Проверим граф на связность: для каждой вершины v должно выполняться used[v] = 2.
if (f)
for(i = 1; i
<= n; i++)
f &= (used[i] == 2);
Выводим ответ. Функция print выводит
длинное число q – кактусность графа.
if (f)
print();
else
printf("0\n");